This is the second followup of an earlier blog article “A perfect storm in a cup of salt water?“
I did an experiment to investigate the relationship of the salt concentration with the mysterious temperature gradient in a cup of salt water. The experiment was to measure the top-bottom temperature differences in three cups of salt water: low-concentration, medium-concentration, and saturated solution. In the saturated solution, there is a salt precipitate at the bottom of the cup. In all measurements, a fast-response temperature sensor was moved up and down in a cup. And the solutions had existed for over 100 hours to ensure that the salt was completely dissolved and the systems had reached thermal equilibrium with the environment.
 The results shown in the graph above clearly indicate that the temperature gradient exists only in the saturated solution. The two unsaturated solutions exhibit no appreciable temperature gradients and measure approximately the same temperature with plain water.
The results shown in the graph above clearly indicate that the temperature gradient exists only in the saturated solution. The two unsaturated solutions exhibit no appreciable temperature gradients and measure approximately the same temperature with plain water.
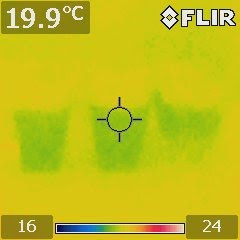
The results were confirmed by an IR image shown above (from left to right: low-concentration, medium-concentration, and saturated).
This experiment suggests that there is probably no ion gradient in an unsaturated solution. An unsaturated salt solution has the same temperature everywhere and that temperature is the same as that of the plain water, whatever its concentration is. I originally expected that an unsaturated solution would have a temperature gradient more or less proportional to the salt concentration, as would a colligative property. This surprising result made me think that the prime suspect is the salt precipitate at the bottom of the cup. We know there is a lot going on on the surface of the precipitate layer. The dissolving and crystallization never cease. It is just that the two processes reach a dynamic equilibrium–the rate of dissolving becomes the same as the rate of crystallization. Sort of like what is shown below:
Let’s think a bit more about the meaning of this experiment. Notice that the temperature curve of the saturated solution lies entirely between that of the ambient temperature and that of the pure water temperature in the graph. This means that the existence of the precipitate somehow weakens the evaporative cooling effect, and probably the evaporation process itself. Why would the evaporation of water at the top of the solution slow down in the presence of some precipitate at the bottom? Exactly how does this process contribute to the temperature gradient existing in the solution?
We can plausibly reason that the rate of evaporation decreases because the ions somewhat act as binding agents that hold the water molecules more tightly through the strong electrostatic attractions. This is known as the water shell effect—water molecules are attracted to an ion and form a dynamic shell around it. As a result, it is more difficult for water molecules to leave the solution to evaporate. But this picture cannot explain why there is virtually no difference between the temperature of a cup of pure water and the temperature of a cup of unsaturated salt water.
It seems the mystery is far from being uncovered. While clarifying a few things, this experiment makes the phenomenon more baffling. Stay tuned for our next investigation.
In terms of its other implications, there is one thing that we can rule out now. There is no such effect in the ocean, as sea water is not saturated.
